第5页(2/2)
每当前述的化装舞会rdquo;发生时,又会变为:
D=(c)
本章已阅读完毕(请 击
击 一章继续阅读!)
一章继续阅读!)
上 写着:──综上所述,由萤幕记录判断,可知在
写着:──综上所述,由萤幕记录判断,可知在
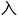 lsquo;房间rsquo;完毕后,至lsquo;隔离墙rsquo;发生的短暂时间
lsquo;房间rsquo;完毕后,至lsquo;隔离墙rsquo;发生的短暂时间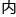 ,各人所在位置将决定lsquo;组合rsquo;之型态。rdquo
,各人所在位置将决定lsquo;组合rsquo;之型态。rdquo
C=(b)
D=(b)
A=(c)
而人格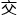 换也确实能在三者以上的人类之间成立。计画小组将两者之间的现象称为筷
换也确实能在三者以上的人类之间成立。计画小组将两者之间的现象称为筷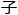 (Chopstick)rdquo;,三者以上的现象称为八爪rdquo;,以示区别。附带一提,这个称呼是艾克洛博士在日本料理店拿着不惯用的筷
(Chopstick)rdquo;,三者以上的现象称为八爪rdquo;,以示区别。附带一提,这个称呼是艾克洛博士在日本料理店拿着不惯用的筷 (Chopstick)吃生章鱼(Octopus)切片时想
(Chopstick)吃生章鱼(Octopus)切片时想 来的,但这个事实却意外地鲜为人知。
来的,但这个事实却意外地鲜为人知。
B=(d)
而人格 换成立后,变为:
换成立后,变为:
接着变为:
对换圆(Switch Circle)rdquo;原来似乎是被设计为双人 换人格用的装置rdquo;(姑且不论是否为外星人所设计);其证据便是隔离墙rdquo;正好将房间rdquo;一分为二,以两个半圆的形式呈现。
换人格用的装置rdquo;(姑且不论是否为外星人所设计);其证据便是隔离墙rdquo;正好将房间rdquo;一分为二,以两个半圆的形式呈现。
D=(d)
D=(a)
真的hellip;hellip;rdquo; 夫隔着博士的肩膀窥探资料,歪了歪
夫隔着博士的肩膀窥探资料,歪了歪 。是这样决定lsquo;组合rsquo;型态的吗?rdquo
。是这样决定lsquo;组合rsquo;型态的吗?rdquo
B=(c)
B=(b)
A=(b)
举例来说,假如人格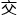 换的成立人数为四人,每个人的
换的成立人数为四人,每个人的
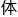 各以A、B、C、D,而
各以A、B、C、D,而 神各以(a)、(b)、(c)、(d)表示;这么一来,原来的
神各以(a)、(b)、(c)、(d)表示;这么一来,原来的 况是:
况是:
示意。
然而,目前的 况显示,不光是化装舞会rdquo;的顺序,连最初的组合rdquo;似乎都有一定的规则
况显示,不光是化装舞会rdquo;的顺序,连最初的组合rdquo;似乎都有一定的规则 。博士不得不承认,这确实
。博士不得不承认,这确实 有将自己从假期中
有将自己从假期中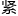 急召回的价值。
急召回的价值。
然而,即使三个以上的人类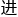
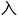 ,对换圆rdquo;仍可
,对换圆rdquo;仍可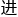 行
行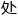 理。虽然隔离墙rdquo;依旧维持原状,房间中央却会有一
理。虽然隔离墙rdquo;依旧维持原状,房间中央却会有一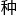 被称为辅助线rdquo;的屏障,
被称为辅助线rdquo;的屏障,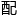 合
合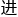
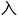 的人数随时
的人数随时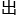 现,将他们分开。若从上方俯瞰,就像是圆形
现,将他们分开。若从上方俯瞰,就像是圆形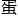 糕被切块一般。
糕被切块一般。
C=(c)
A=(a)
B=(a)
之后一度变回正常状态,接着又以这个顺序重复发生化装舞会rdquo;。这么看来,便可明白化装舞会rdquo;的替换顺序是依次往后递延一位。
C=(a)
不过,以这四人组为例;过去计画小组一直认为八爪rdquo;的最初组合rdquo;是以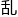 数
数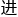 行的,因此无法将特定的受试者转移至A或B
行的,因此无法将特定的受试者转移至A或B 上。
上。
C=(d)
A=(d)